Basic hooter whistle

By Johan Liljencrants

This note provides a few design parameter details for a basic single note whistle. The scope is limited since a couple of those parameters are very specific, based on custom and experience. Namely that the whistle diameter is one third of its length, and that the mouth extends all around and has the same area as the bell.

The design is illustrated with an air blown prototype, constructed from PVC drainage pipes. A simple trick is shown, by which you can simulate the pitch bend characteristic of steam blowing.

1. The whistle parts

This general drawing includes two ways to hold parts together. These are examples of how you could do, but they can be varied at will depending on fabrication facilities and taste.

The most basic part is the bell, a tube that is closed at its top end, open at bottom. Its bottom rim forms the upper lip of the mouth of the whistle. The upper lip is usually somewhat sharpened with a bevel typically at an angle of 30 degrees. Neither this angle or the sharpness of the edge is critical.

Blowing air or steam enters through the bottom bowl, or foot. The upper rim of the foot has the same diameters as the bell and forms the lower lip of the whistle. Most of the foot top is covered by a round disk, the languid, normally with a slightly beveled edge. The diameter of the languid is somewhat smaller than the inside of the foot, leaving a narrow slit, the flue. Through this the blowing air/steam forms a jet across the mouth, heading toward the outside of the upper lip. This jet is the driving agent for the whistle as its direction alternates between inside and outside of the upper lip.

In most classical whistles the bell is held in place by a rigid central post, the right alternative here. The lower anchor point of the post is complicated in that it must stay clear of the flue and leave a free path for the blowing medium. The upper lip must be accurately aligned above the slit. For that reason it may be good to put a ruggedizing spider inside the lower part of the bell.

The left design has no post, popular when whistles are made from tubes. Instead the bell is anchored to the foot by three or more wings, running outside as bridges across the mouth. Another variation may be to reduce the mouth width to occupy e.g. half or a quarter of the circumference, like in organ pipes, such that the bowl and bell are parts of the same tube. This however reduces the sound volume.

2. Critical dimensions

2.1 Length

The most basic measure is the length L, internally from the closed top of the bell down to the languid plate. This sets the pitch of the whistle, it closely equals a quarter wavelength of the note produced. The pitch, alternately note, or frequency F, is measured in Hertz, the same as cycles per second. Knowing F you find wavelength as c / F, where c is the speed of sound. The nominal length L of the bell actually has to be made shorter than a quarter wavelength, because air outside the mouth will take part in the resonance motion of the bell air column. For this particular design with 3:1 scale this 'end correction' is empirically about 6%, so the whistle will speak one semitone lower than you might believe from L alone.

For air at 20 centigrade (69 F) sound speed c is 343 meter/second, same as 13500 inches/second. It increases about 0.17 % per degree centigrade (0.10 % per degree F). With steam c is notably higher. Blowing a whistle with steam will heat it gradually, and this together with the expulsion of its air produces a characteristic pitch bend at the tone start. For steam you can not tell an accurate value, but we can assume an approximate average of c to be 400 meter/second, or 15750 inches/second. This represents a upward shift of about 2.7 semitones relative to air.

The following set of scales relate note to length L, valid for air, and including the mentioned end correction. Put a vertical line at some quantity you know and read corresponding values of the others. For example, for a keyhole C frequency is 260 Hz, and L is 12 inches or 305 mm. The little top right indicator shows how much to shift the upper L scales to the right in order to use them for steam. The same length will then rather produce a 305 Hz #D. Or that same C will then require L to be 14 inches, or 356 mm.

2.2 Diameter

The ratio of length L to diameter D is called the scale of the pipe. This may be varied at will by the designer. A narrower scale makes the tone contain stronger harmonics to the fundamental, a feature much used in organ pipe design. In the same time this increases its tendency to overblow, that is, the fundamental is lost and the pipe will speak at a harmonic instead. But with whistles a main concern is loudness and no overblowing. Experience then tells that a good rule is to select a 3:1 scaling, diameter D should be one third of the length L, D = L/3. We stay with this rule here.

2.3 Mouth

The next general recommendation for a loud whistle is that the mouth area should be about the same as the bell cross section. For the basic design with 3:1 scale and a mouth extending all around the bell this automatically means the cut up H should be one twelwth of the length, H = L/12 = D/4. With a lower cut up you must hold back blowing power to avoid overblowing, and with a higher one the jet loses relatively more of its energy into turbulence under way to the upper lip.

2.4 Flue

In the flue the static energy of the blowing medium, represented by its pressure P, is converted into kinetic energy in form of speed V. This conversion obeys the Bernoulli equation P = 0.5 * r * V², where r is the density of the medium. In his research on organ pipes Hartmut Ising once defined an 'intonation number', a formula to determine a best slit width T, depending on cut up H, jet speed V, and pitch F (for a general dimensioning chart see [1]).

Using the Bernoulli equation and our present specific assumptions of a 3:1 scale, a 360 degree mouth of same area as the bell, and with intonation number 2.5 this boils down to the simple formula PT = 25L, using SI units. This tells two essential things. One is that the slit width T should be set in proportion to L, the other that it should be inversely proportional to pressure P. The formula is graphically shown by the black sloping lines in the following diagram.

For a particular whistle, draw a horizontal line at its actual L, displayed at left. On this line, the black lines form scale marks for slit width T against the bottom pressure P scale.

From the pressure, slit width and diameter one can also compute the power delivered by the blowing air and its flow rate. Supply power is shown by the red lines. In an efficiently working whistle the typical acoustic output power is about 1 % of that input. Flow rate is shown by the blue lines.

This diagram, derived from the Ising equation, may rouse some discussion. For instance, its description of T vs. P differs very substantially from what is given in [2]. It is unclear if there is a theoretical background to that practice, but obviously the pressures in classical steam whistle applications are vastly higher than in organs. No doubt sound level can increase with higher blowing pressure, but most likely efficiency (the fraction of supplied power that is actually converted into sound) goes down. With pressures approaching and beyond atmospheric, then common linear acoustics relations are no more accurately valid. It is also very common that high pressure pipes are overblown. To cure overblowing one remedy is to decrease slit width, but this may soon reach a practical limit for reasons of mechanical tolerance. A more drastic means is to increase cut up.

2.5 Inlet and valve

When the blowing medium passes a constriction its pressure is reduced in proportion to its linear speed squared, as described by the Bernoulli equation above. One issue may be that the medium should find no essential constriction on its way to the flue, because that will reduce the power available to the whistle in relation to what is supplied by the blower. If we assume that the passage has a single constriction area A while the flue has area B (slit width times circumference), then the fraction of pressure lost can be formulated as B²/(A²+B²). If A=B, then the loss is 50%, but increasing the constriction area A e.g. three times will reduce the loss into only 10%. One can adopt the latter as a rule of thumb: any constriction in the feeding path, like inlet or valve diameter, should have a cross sectional area that is at least three times larger than the flue area.

Presumably, with steam driven train whistles and the like, the foot pressure is substantially lower than the boiler supply pressure, due to the throttling action of a narrow valve passage. As a counter example using the formula above, if valve area A is one third of flue area B, then foot pressure is only 10% of the supply pressure.

3. Note on pitch and end correction

It was mentioned that blowing with steam will cause a gradual pitch rise as the pipe heats and the medium is changed. A similar rise comes with air, but to a lower degree, see e.g. [3]. The cause of this can be attributed to two factors.

One is related to the energy transfer from the flue jet to the resonator. The resonating air column in the bell makes for a flow oscillating in and out through the mouth. This flow controls the direction of the flue jet to tend alternately toward the inside and outside of the upper lip. This mechanism incorporates a delay that depends on the speed of the jet, hence also to pressure, it is related to the transit time for the jet across the mouth. The delay corresponds to a certain phase angle at the oscillating frequency. At stable oscillation there is a match between this 'jet phase' angle and the phase of the resonating column i the bell, such that energy is transferred from jet to column. Precisely at the bell resonance its phase angle is zero, by definition. The 'jet phase' makes the oscillation frequency deviate somewhat from that bell resonance, to an extent varying with pressure. - This complicated theory, here briefly outlined, is one base for the Ising formula.

The other factor may be coined as 'the blown away end correction'. In classical acoustic theory the length of the resonator tube is apparently incremented by 0.6 times its radius. This is because the medium outside the open tube end takes part in the resonance motion. Now, with the jet traversing the resonator end this external air is partially swept away, the oscillation energy in the outward bound puffs is lost to the resonator. This means the end correction becomes smaller because of the crossing jet flow, and also the resonance Q lowers. Since the end correction is proportional to tube radius this effect is larger in wide scale whistles.

This mentioned classical end correction for a tube comes when mouth area equals the tube area. In some whistles and most organ pipes the mouth area is however considerably smaller. Then one might believe the end correction would also get smaller. But actually the opposite will happen - a narrower mouth will act as an additional acoustic mass to make the tube virtually longer and lower the pitch produced. Ingerslev and Frobenius (1947) gave an empirical formula for the effective end correction dL_m when the mouth area S_m is much smaller (<0.25) than the tube area S, namely dL_m = 0.73*S/sqrt(S_m). For larger mouth areas you gradually reach the classical straight tube end correction dL = 0.6*r = 0.34*sqrt(S).

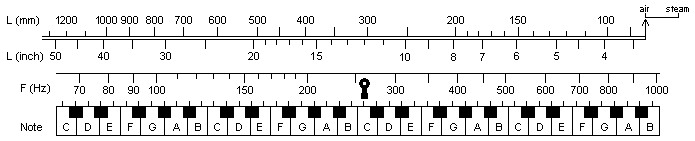
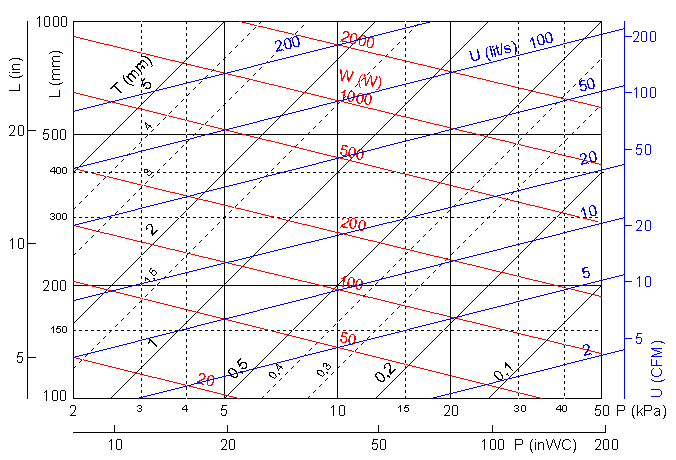
4. Demonstration model

This photo shows two rather unromantic whistles fabricated like in the drawing above, from 75 and 50 mm (3 and 2 inch) PVC drainage tubing. The internal disks are turned from 1/2 inch plywood to press fit tolerance. Their notes using the 3:1 scaling rule form the fifth interval G and D. Since the bell tubes are made with about 30% excess length they can be tuned down as far as to a fourth lower by pushing up their top disks to increase L.

These two whistles were simultaneously blown from an industrial fan that delivers about 4 kPa pressure (17 inWC, 0.6 PSI) which results in about 115 dBC sound pressure level at 1 meter distance. Slit widths are 1.0 and 0.8 mm respectively. The whistles are connected to the fan with a T joint, such that the fan is free blowing through the third opening of the joint. The whistles sound when this opening is covered with the hand. In the sample the higher whistle is tuned down to #C to form a diminished fifth interval.

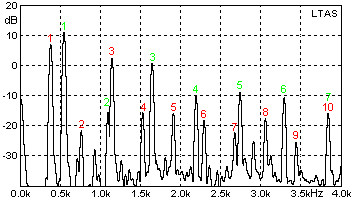The sound clip was recorded at 6 m distance from the whistles, outdoors facing a park. Background is some reverberation from surrounding houses and a weak titter from sparrows.

In this spectrum of the sound the harmonic numbers for the 3 inch whistle 370 Hz G are identified with red figures. Harmonics for the 2 inch 550 Hz #C with green.

5. Steam simulator trick

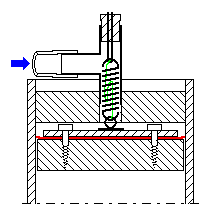
Blowing with steam the initial pitch rise makes for an appealing howl characteristic that is less pronounced using air. This sketch shows a workaround to increase the glide with air. Below the top of the bell a gasketed (red) piston is added, with a spring pulling it upward. The space between top and piston is connected with a tube to the foot of the whistle. When blowing pressure (blue) is turned on, the piston moves down such that the effective bell length is reduced and pitch rises. Unless you have close control of spring force, piston area, and pressure it is wise to limit the piston travel with a thread or chain inside the spring (green).

This sound clip illustrates the action with the 3" whistle alone. It was tuned down to about E which reduced sound level to 107 dBC at 1 m distance.

6. References

[1]   'Pipe cut-up and flue pipe dimensioning chart', in Mechanical Music Digest, Technical gallery: http://www.mmdigest.com/Tech/isint.html
[2]   'Slit width vs pressure .xls', inYahoo steam-whistles group: http://groups.yahoo.com/group/steam-whistles/files/
[3]   'Scale v frequency stability.jpg', inYahoo steam-whistles group: http://groups.yahoo.com/group/steam-whistles/files/
[4]   Ingersev, Frobenius (1947): Trans. of the Danish Academy of Technical Sciences, No. 1.

Johan Liljencrants 2006-02-24