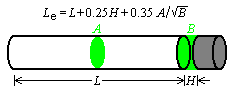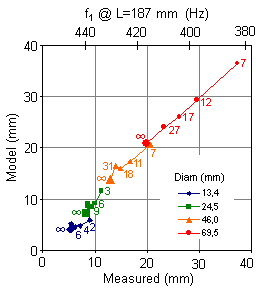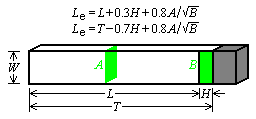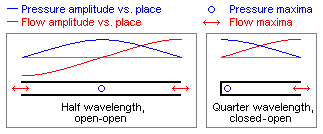
Let us initially inspect a quarter
wavelength
resonator tube of length L
and area A,
closed at one
end. This tube has a total
acoustical
mass
and acoustical capacitance
,
where
is density of the air
and c is its
speed of sound.
The effective resonating mass and capacitance
are less than these total
ones. They are reduced by the
factor
due to the sinusoidal distribution within the tube of
flow
and pressure. (This factor is the area of a sine
quadrant, divided by
the area of its circumscribed rectangle). Thus the effective mass is
and
effective
capacitance
.
Inserting these into the resonance formula
and
cleaning up, leads into the well known
quarter wave expression
for
the fundamental
resonance.

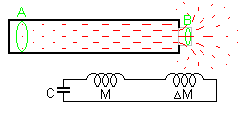 There
is a paradox
in that the basic correction formula for
the
There
is a paradox
in that the basic correction formula for
the 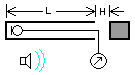 A number of
tubes with one end closed were examined for their passive
fundamental
resonances. The open ends were adjustable for variation in
cutup H.
A number of
tubes with one end closed were examined for their passive
fundamental
resonances. The open ends were adjustable for variation in
cutup H.